Los números complejos expresan la suma entre un numero real y un número imaginario. Un número real es aquel que puede ser expresado por un numero entero (4, 15, 2686) o decimal (1,25; 38,1236; 29854,152). En cambio, un número imaginario es unnumero cuyo cuadrado es negativo. El concepto de número imaginario fue desarrollado por Leonhard Euler en 1777, cuando le otorgó a √-1 el nombre de i (de “imaginario”).
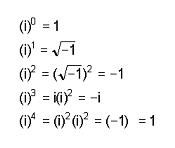
La
noción de número complejo aparece ante la imposibilidad de los números
reales de expresar las raíces de orden par de los números negativos. Los
números complejos pueden expresar todas las raíces de los polinomios, algo que los números reales no están en condiciones de hacer.
De esta forma, los números complejos se usan en diversos campos de las matemáticas, en la física y en la ingeniería.
Gracias a su capacidad para representar la corriente eléctrica y las
ondas electromagnéticas, son utilizados con frecuencia por la electrónica y las telecomunicaciones.
El cuerpo de los números reales está formado por pares ordenados (a, b). El primer componente (a) es la parte real, mientras que el segundo componente (b) es la parte imaginaria. Los números imaginarios puros son aquellos que sólo están formados por la parte imaginaria (por lo tanto, a=0).
Los números complejos forman el cuerpo complejo (C). Cuando el componente real a es identificado con el complejo (a, 0), el cuerpo de los números reales (R) aparece como un subcuerpo de C. Por otra parte, C forma un espacio vectorial de dos dimensiones sobre R. Esto demuestra que los números complejos no pueden ser ordenados, a diferencia de los números reales.
Cada número complejo puede ser escrito unívocamente como una suma de un número real y un número imaginario, de esta forma:
Al número imaginario i se le denomina también constante imaginaria.
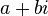
al conjunto de los 
.
es una especie de anfibio entre el ser y la nada.
No hay comentarios:
Publicar un comentario